Bài viết này tổng hợp toàn bộ các công thức hình học không gian lớp 12 quan trọng, giúp bạn nắm vững kiến thức và giải quyết các bài toán một cách hiệu quả. Nội dung được sắp xếp logic, dễ hiểu, giúp bạn ôn tập và củng cố kiến thức một cách hệ thống. Thành công trong học tập cũng là một công thức để làm giàu kiến thức, mở ra nhiều cơ hội trong tương lai. Hãy cùng khám phá!
Khối Đa Diện
Khối đa diện là phần không gian giới hạn bởi một hình đa diện. Bao gồm các hình chóp tam giác, chóp tứ giác, hình hộp… Công thức tính thể tích khối chóp (áp dụng cho cả chóp tam giác và tứ giác) như sau:
Thể tích khối chóp: V = (1/3) * S_đáy * h
Trong đó:
S_đáy: Diện tích mặt đáy.h: Độ dài chiều cao.
Thể tích khối chóp S.ABCD được tính bằng công thức: V_{S.ABCD} = (1/3)d(S,(ABCD)) * S_{ABCD}
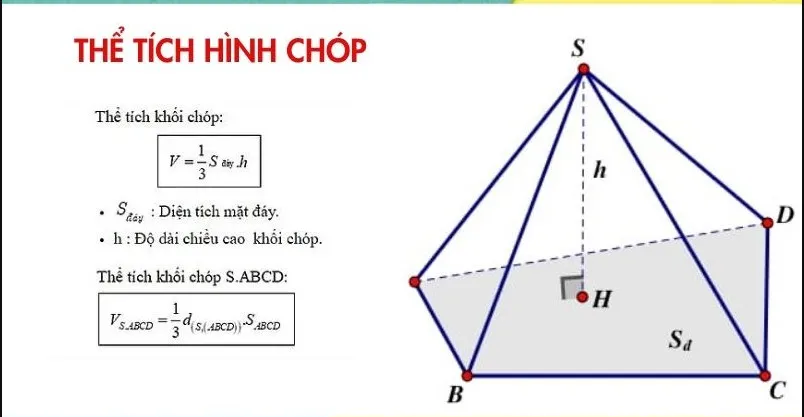Công thức thể tích khối chóp
Thể tích khối lăng trụ: V = S * h
Trong đó:
S: Diện tích đáy.h: Chiều cao.
Lưu ý: Hình lăng trụ đứng có chiều cao chính là cạnh bên. Bạn có thể tham khảo thêm công thức tính thể tích khối lăng trụ tam giác đều để giải các bài tập về hình lăng trụ. Việc hiểu rõ các công thức này sẽ giúp bạn vững vàng hơn trong con đường chinh phục kiến thức, một bước đệm quan trọng trong việc xây dựng sự nghiệp và làm giàu.
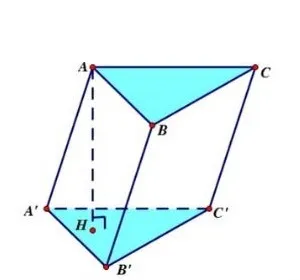Công thức thể tích khối lăng trụ
Thể tích hình hộp chữ nhật: V = a * b * c (a, b, c cùng đơn vị)
Hình lập phương là trường hợp đặc biệt của hình hộp chữ nhật với a = b = c. Do đó, thể tích hình lập phương được tính bằng công thức: V = a³
Công thức thể tích hình hộp chữ nhật
Khối Chóp Cụt
Khối chóp cụt nằm giữa mặt đáy và thiết diện cắt bởi đáy của hình chóp và một mặt phẳng song song với đáy.
a) Diện tích xung quanh hình chóp cụt: S_{xq} = n * S_{mtb} hoặc S_{xq} = n * (1/2) * (a + b) * h
Trong đó:
S_{xq}: Diện tích xung quanh.n: Số lượng mặt bên.a, b: Chiều dài cạnh của 2 đáy trên và dưới của hình chóp cụt.h: Chiều cao mặt bên.
b) Diện tích toàn phần hình chóp cụt: S_{tp} = S_{xq} + S_{đáy lớn} + S_{đáy nhỏ}
c) Thể tích hình chóp cụt: V = (1/3)h(S + S' + √(S*S'))
Trong đó:
V: Thể tích hình chóp cụt.S, S': Lần lượt là diện tích mặt đáy lớn và đáy nhỏ của hình chóp cụt.h: Chiều cao (khoảng cách giữa 2 mặt đáy lớn và đáy nhỏ).
Công thức hình chóp cụt
Muốn thành công trong kinh doanh, bạn cần phải có kiến thức vững chắc như nắm vững các công thức hình học này. Hãy học hỏi liên tục và áp dụng kiến thức vào thực tiễn để đạt được mục tiêu tài chính của mình. Bạn có thể tham khảo thêm về các loại bảo hiểm bắt buộc để bảo vệ tài sản của mình.
Hình Nón
a) Diện tích xung quanh hình nón: S_{xq} = π * r * l
Trong đó:
S_{xq}: Diện tích xung quanh.r: Bán kính đáy hình nón.l: Đường sinh của hình nón.
b) Diện tích toàn phần hình nón: S_{tp} = S_{xq} + S_{đáy} = π * r * l + π * r²
c) Thể tích khối nón: V = (1/3) * π * r² * h
Trong đó:
V: Thể tích khối nón.h: Đường cao tính từ đỉnh hình nón xuống tâm đường tròn đáy.
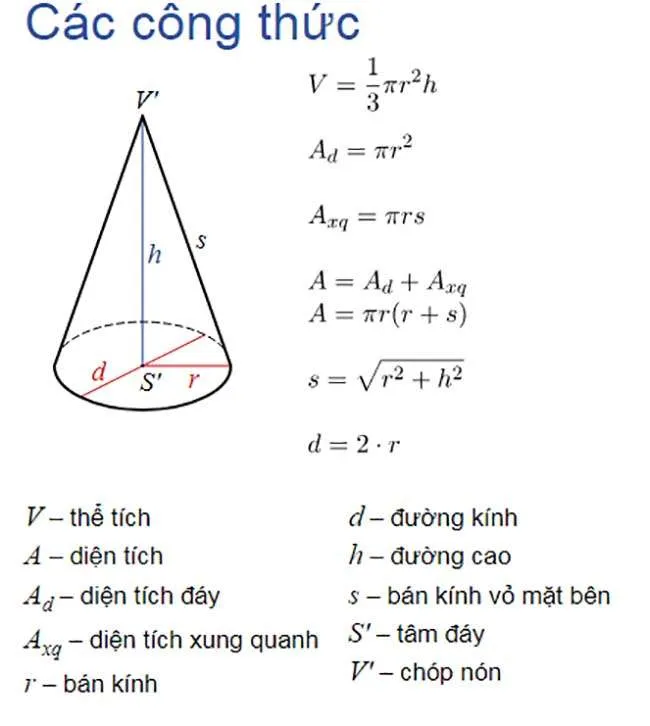Công thức hình nón
Bạn đang tìm hiểu về các công thức toán học để nâng cao kiến thức? Đừng bỏ qua công thức xác suất 11 để mở rộng hiểu biết của mình.
Hình Trụ
a) Thể tích khối trụ: V = π * r² * h = h * S_đáy
Trong đó:
r: Bán kính hình trụ.h: Chiều cao hình trụ.
b) Diện tích xung quanh khối trụ: S_{xq} = 2 * π * r * h
c) Diện tích toàn phần: S_{tp} = S_{xq} + 2 * S_đáy = 2πrh + 2πr²
Để có cuộc sống giàu có, bạn cần có chiến lược kinh doanh tốt. Việc học hỏi không ngừng sẽ giúp bạn có cái nhìn tổng quan hơn, giống như việc hiểu rõ tất cả các công thức trong toán học vậy. Hãy tham khảo thêm bài viết về Ngô Thời Nhiệm Bình Tân để hiểu thêm về một chiến lược kinh doanh thành công.
Mặt Cầu
Cho mặt cầu S(I, R), ta có:
- Diện tích mặt cầu:
S = 4πR²
Tọa Độ Trong Không Gian
Hệ tọa độ Oxyz
Vectơ
Tích có hướng của 2 vectơ
Tọa độ điểm
Phương trình mặt cầu, đường thẳng, mặt phẳng
(Phần này giữ nguyên nội dung gốc, nhưng cần được viết lại bằng tiếng Việt chuẩn xác và tự nhiên hơn, đồng thời lồng ghép các liên kết nội bộ một cách khéo léo.)
Bạn có thể tìm hiểu thêm về cách sử dụng công cụ hỗ trợ như CHÁT GPT: Hướng dẫn đăng ký và sử dụng thành công 100% để hỗ trợ công việc học tập của mình. Hiểu rõ các công thức toán học không chỉ giúp bạn trong việc học tập mà còn là nền tảng cho việc đưa ra các quyết định kinh doanh chính xác hơn. Hãy tìm hiểu thêm về công thức tính C phần trăm để áp dụng vào việc phân tích dữ liệu kinh doanh.