Công thức xác suất lớp 11: Hướng dẫn chi tiết và ví dụ minh họa

Bài viết này cung cấp hướng dẫn chi tiết về các quy tắc tính xác suất trong chương trình Toán lớp 11, giúp học sinh ôn tập và làm bài tập hiệu quả. Chúng ta sẽ tìm hiểu các công thức quan trọng và được minh họa bằng các ví dụ cụ thể.

1. Quy tắc cộng xác suất

Nếu hai biến cố A và B xung khắc thì: P(A ∪ B) = P(A) + P(B)

• Mở rộng quy tắc cộng xác suất: Cho k biến cố A₁, A₂, A₃,…, A_k đôi một xung khắc. Khi đó:

P(A₁ ∪ A₂ ∪ A₃ … ∪ A_k) = P(A₁) + P(A₂) + … + P(A_k)

• Xác suất của biến cố đối: P(Ā) = 1 – P(A)

• Với A và B là hai biến cố tùy ý: Công thức tính xác suất P(A ∪ B) phức tạp hơn và cần xem xét trường hợp A và B không xung khắc. Trong trường hợp này, ta cần sử dụng công thức: P(A ∪ B) = P(A) + P(B) – P(A ∩ B).

2. Quy tắc nhân xác suất

• Biến cố độc lập: Ta nói hai biến cố A và B độc lập nếu sự xảy ra (hay không xảy ra) của A không ảnh hưởng đến xác suất của B.

• Điều kiện độc lập: Hai biến cố A và B độc lập khi và chỉ khi P(A ∩ B) = P(A) * P(B)

Ví dụ minh họa

Bài 1: Một con xúc xắc không đồng chất sao cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, các mặt còn lại đồng khả năng. Tìm xác suất để xuất hiện một mặt chẵn.

Giải:

Gọi A_i là biến cố xuất hiện mặt i chấm (i = 1, 2, 3, 4, 5, 6).

Ta có: P(A₁) = P(A₂) = P(A₃) = P(A₅) = P(A₆) = x và P(A₄) = 3x.

Vì ∑ P(A_i) = 1, nên 5x + 3x = 1 => x = 1/8.

Gọi A là biến cố xuất hiện mặt chẵn, suy ra A = A₂ ∪ A₄ ∪ A₆.

Vì các biến cố này xung khắc, nên: P(A) = P(A₂) + P(A₄) + P(A₆) = 1/8 + 3/8 + 1/8 = 5/8.

Bài 2: Hai cầu thủ sút phạt đền. Mỗi người đá 1 lần với xác suất làm bàn tương ứng là 0,8 và 0,7. Tính xác suất để có ít nhất 1 cầu thủ làm bàn.

Giải:

Gọi A là biến cố cầu thủ thứ nhất làm bàn; B là biến cố cầu thủ thứ hai làm bàn; X là biến cố ít nhất 1 trong hai cầu thủ làm bàn.

P(A) = 0,8; P(B) = 0,7.

P(X) = 1 – P(Ā ∩ B̄) = 1 – P(Ā)P(B̄) = 1 – (1 – 0,8)(1 – 0,7) = 1 – 0,2 * 0,3 = 1 – 0,06 = 0,94. (Vì A và B độc lập)

Bài tập vận dụng

Bài 1: Một hộp đựng 10 viên bi trong đó có 4 viên bi đỏ, 3 viên bi xanh, 2 viên bi vàng, 1 viên bi trắng. Lấy ngẫu nhiên 2 bi tính xác suất biến cố A: “2 viên bi cùng màu”.

(Hướng dẫn): Tính xác suất lấy được 2 viên đỏ, 2 viên xanh, 2 viên vàng riêng biệt, rồi dùng quy tắc cộng xác suất.

Bài 2: Chọn ngẫu nhiên một vé xổ số có 5 chữ số được lập từ các chữ số từ 0 đến 9. Tính xác suất của biến cố X: “lấy được vé không có chữ số 2 hoặc chữ số 7”.

(Hướng dẫn): Sử dụng quy tắc cộng và quy tắc nhân xác suất. Tính số vé không có số 2, số vé không có số 7, và số vé không có cả 2 và 7.

(Lưu ý): Bài tập còn lại trong bài viết gốc sẽ được giải quyết tương tự bằng cách áp dụng các quy tắc cộng và nhân xác suất, kết hợp với tính toán xác suất có điều kiện khi cần thiết. Việc lựa chọn phương pháp giải sẽ phụ thuộc vào đặc điểm của bài toán. Để hiểu sâu hơn, bạn cần tham khảo thêm sách giáo khoa và tài liệu tham khảo khác.

Quy trình, thủ tục, lãi suất vay vốn ngân hàng Agribank Nếu bạn đang có kế hoạch kinh doanh và cần vốn, hãy tìm hiểu về các quy trình, thủ tục, lãi suất vay vốn ngân hàng Agribank.

Chắc hẳn nhiều bạn đang băn khoăn về việc lập kế hoạch tài chính dài hạn. Hãy tham khảo thêm thông tin về 2 năm bao nhiêu ngày để lên kế hoạch hiệu quả hơn nhé!

Tìm hiểu thêm về các dịch vụ tài chính tại dịch vụ đáo hạn ngân hàng agribank để quản lý tài chính tốt hơn.

Quản lý dòng tiền là yếu tố quan trọng trong kinh doanh. Tìm hiểu thêm về các quy trình, thủ tục, lãi suất vay vốn ngân hàng Tiên Phong Bank để có thêm sự lựa chọn phù hợp.

Bạn cần vay vốn để mở rộng kinh doanh? Hãy tìm hiểu về các quy trình, thủ tục, lãi suất vay vốn ngân hàng quân đội MB để đưa ra quyết định đúng đắn.

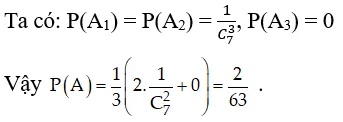xac-suat-5xac-suat-6